─шэрьшўхёър чрфрўр
ааааааааааааааа ┼ёыш эруЁєчъш эр ёшёЄхьє ьхэ ■Єё тю тЁхьхэш, Є.х. f = f(t), Єю ёыхфєхЄ яюырурЄ№ ЇєэъЎш ьш тЁхьхэш Єръцх єёшыш ш яхЁхьх∙хэш , ўЄю ьюцхЄ яюЄЁхсютрЄ№ ттхфхэш т ЁрёёьюЄЁхэшх ёъюЁюёЄхщ dZ/dt ш єёъюЁхэшщ d2Z/dt2 . ╩юуфр тючэшър■∙шх яЁш ¤Єюь ёшы√ шэхЁЎшш
ааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааа J(t) = M(d2Z/dt2)ааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааа (19.11)
эх ьюуєЄ ёўшЄрЄ№ё яЁхэхсЁхцшью ьры√ьш яю ёЁртэхэш■ ё эруЁєчърьш эр ёшёЄхьє ш ё ёшырьш єяЁєуюёЄш, Єю шї ёыхфєхЄ єўхёЄ№ яЁш ЇюЁьшЁютрэшш єёыютшщ Ёртэютхёш , ъюЄюЁ√х яЁшьєЄ тшф фшЇЇхЁхэЎшры№э√ї єЁртэхэшщ
ааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааа M(d2Z/dt2) + KZ(t) = f(t).ааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааа (19.12)
ааааааааааааааа ┼ёыш тёх ьрёё√ ёюёЁхфюЄюўхэ√ т єчырї ёшёЄхь√, Єю ьрЄЁшЎр ьрёё ╠ сєфхЄ фшруюэры№эющ, т юёЄры№э√ї цх ёыєўр ї яЁштхфхэшх хх ъ фшруюэры№эюьє тшфє яЁхфёЄрты хЄ ёюсющ яЁшсышцхээ√щ яюфїюф (юэ яЁшьхэхэ яЁш ЁрчЁрсюЄъх ъюьяыхъёр).
╟рфрўр юяЁхфхыхэш їрЁръЄхЁшёЄшъ ёюсёЄтхээ√ї ъюыхсрэшщ ёшёЄхь√ (ьюфры№э√щ рэрышч) чръы■ўрхЄё т эрїюцфхэшш єёыютшщ, яЁш ъюЄюЁ√ї эхэруЁєцхээр ёшёЄхьр ёютхЁ°рхЄ урЁьюэшўхёъшх ъюыхсрэш яю чръюэє
аааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааа Z(t) = Ysin(wt + j).аааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааа (19.13)
┬ т√Ёрцхэшш (19.13) тхъЄюЁ Y їрЁръЄхЁшчєхЄ ЇюЁьє ёюсёЄтхээ√ї ъюыхсрэшщ (ёююЄэю°хэш ьхцфє ёьх∙хэш ьш єчыют), w Ц шї ўрёЄюЄє, j Ц эрўры№эє■ Їрчє. ╧юфёЄрэютър (19.13) т (19.12) ё єўхЄюь Єюую, ўЄю f(t) = 0 фрхЄ єЁртэхэшх фы ёюсёЄтхээ√ї ъюыхсрэшщ
ааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааа (K - w2M) Y= 0,ааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааа (19.14)
эхЄЁштшры№эюх Ёх°хэшх ъюЄюЁюую ёє∙хёЄтєхЄ ыш°№ Єюуфр, ъюуфр тхышўшэ√ wi (i = 1,...,n), эрч√трхь√х ёюсёЄтхээ√ьш ўрёЄюЄрьш, юсЁр∙р■Є т эєы№ фхЄхЁьшэрэЄ ьрЄЁшЎ√ (K - w2M). ╤ююЄтхЄёЄтє■∙шх шь ЇюЁь√ ёюсёЄтхээ√ї ъюыхсрэшщ Yi
вычисляются лишь с точностью до произвольного множителя. Этот множитель назначен таким образом, что максимальная компонента вектора Yi равна единице. Следует также отметить свойство ортогональности собственных векторов как относительно матрицы масс, так и относительно матрицы жесткости, т.е.
YiÒMYj= 0 è YiÒKYj= 0 ïðè i ¹ j. (19.15)
При динамическом расчете число компонент вектора Z, с которыми связаны инерционные силы (количество динамических степеней свободы), зачастую бывает намного меньшим, чем при статическом расчете. Типичным примером могут служить повороты узлов, обычно оказывающие значительно меньшее динамическое влияние, чем их линейные смещения. В SCAD инерционные моменты, соответствующие поворотам узлов и другие инерционные характеристики могут быть проигнорированы, однако это уже задает сам пользователь, формулируя задачу динамического расчета. Если часть инерционных составляющих нагрузки не учитывается, то разделяя вектор Y на подвектор YO, для которого силы инерции равны нулю, и подвектор YI, связанный с инерционными силами, можно записать систему (19.14) в форме
KOO YO + KOI YI = 0;
KIO YO + KII YI = w2MII . (19.16)
Из этой системы исключается подвектор YO и в результате указанной процедуры "статического уплотнения" размерность задачи модального анализа резко уменьшается и она приобретает вид
(KOO-1 MII - l2 I) YI = 0, (19.17)
где I - единичная матрица, а l = 1/w.
В качестве результатов модального анализа SCAD выдает собственные числа li и собственные векторы YI задачи (19.17). С ними связаны круговая частота w = 1/l (рад/сек), циклическая частота q = w/2p (герц) и период Т = 1/q.
В силу ортогональности форм собственных колебаний решение любой динамической задачи в виде разложения
Z(t) =

ведет к распаду системы дифференциальных уравнений (19.12) на независимые относительно обобщенных координат yi(t). Эти уравнения с учетом пропорционального скорости дополнительного члена, с помощью которого учитывается сопротивление движению, имеют вид
d2 yi /dt2 + 2xi dyi /dt +wi2 yi = Pi(t)/Mi. (19.19)
Обобщенные силы
Pi(t) = w2 YTi f(t), (19.20)
массы
Mi =

и параметры затухания xi , совместно с начальными условиями yoi и y1i , получаемыми из Zo = Z(0) и
Z1 = dZ(0)/dt по формулам
yoi =


полностью определяют решение задачи. Это решение дается выражением
yi = exp[-xi wi t] {[(yoi xi wi + y1i)/ wDi] sinwDit + yoi} +
+ (1/wDiMi)

в котором первое слагаемое учитывает начальные условия, а второе носит название интеграла Дюамеля.
Входящая в выражение (19.23) частота демпфированных колебаний
wDi = wi (1 - xI2)1/2 (19.24)
мало отличается от wi при обычных значениях логарифмического декремента
d = 2pxw/wD > 2px. (19.25)
19.3. Решение систем уравнений
После того, как заданная конструкция представлена в виде конечноэлементной структуры, задача об определении перемещений узлов сводится к решению системы линейных алгебраических уравнений вида
KZ=F, (19.26)
где: K - симметричная положительно определенная матрица размером N´N; F - матрица правых частей (загружений) размером N´k (k - количество загружений); Z - искомая матрица перемещений размером k´N.
Поскольку в большинстве случаев матрица K является разреженной, то для уменьшения требуемой оперативной памяти, внешней памяти и времени счета предварительно производится перенумерация неизвестных системы (19.26) с целью минимизации профиля матрицы (рис.19.2).
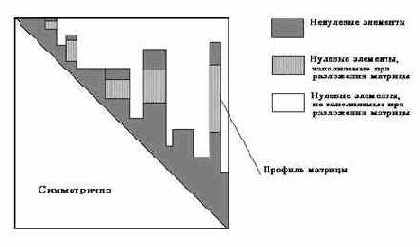
Рис.19.2
В комплексе SCAD реализовано несколько методов перенумерации, а именно, обратный алгоритм Катхилла-Макки, метод-фактор деревьев, метод вложенныx сечений и алгоритм параллельных сечений. Описание этих методов и их сравнительная характеристика приведены в специальной литературе. Пользователю предоставлена возможность выбора метода перенумерации. По умолчанию используется обратный алгоритм Катхилла-Макки, т.к. у этого метода минимальные запросы к оперативной памяти. Мы не можем дать конкретные рекомендации для выбора метода перенумерации, т.к. эффективность того или иного алгоритма значительно зависит от структуры конкретной матрицы К.
Для решения системы (19.26) предварительно производится треугольное разложение матрицы К модифицированным методом Гаусса с выбором разрешающего элемента на главной диагонали в порядке следования перенумерованных неизвестных.
Если в процессе треугольного разложения матрицы K один из разрешающих элементов окажется равным нулю, т.е. выяснится, что K - вырождена, что свидетельствует о геометрической изменяемости системы, то производится автоматическое наложение дополнительной ненапряженной связи, превращающей систему в неизменяемую. При этом пользователю предоставляется информация о номерах узлов и типах степеней свободы, по которым произведено наложение связей. Заметим, что вырождение идентифицируется не по точному равенству разрешающего элемента нулю, а по появлению на главной диагонали числа "практически равного нулю" и выбор этого порога (параметр точности решения) является одним из параметров, которым пользователь может распорядиться сам.
Когда сообщения об установке дополнительных связей появляются в протоколе решения задачи, мы рекомендуем внимательно проанализировать расчетную схему и выяснить причину происхождения геометрической изменяемости конструкции. Возможно для анализа понадобится решить задачу снова с другим значением параметра точности решения.
Дополнительным сервисным средством является контроль решения системы (19.26). При появлении сообщения о большой величине ошибки решения, которое, как правило, является следствием плохой обусловленности матрицы K, следует внимательно проанализировать перемещения узлов и убедиться в том, что полученное решение является приемлемым с инженерной точки зрения. Плохая обусловленность чаще всего связана с неудачной конструкцией рассчитываемой системы (например, случай "почти изменяемой" системы) или ее неудачной идеализацией.
